Some time ago somebody had to solve this math optimization question for their studies and told me about it.
So there is a wall with height h, which has the distance a from a very high "building" and your task, should you accept it, is to find the shortest ladder over the wall that touches the ground and the "building".
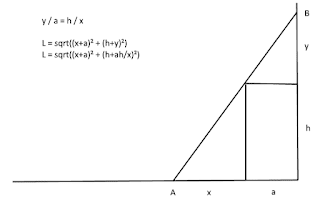
Because we know that y/a = h/x it follows that y = ah/x.
Using this the length become L = sqrt((x+a)^2+(h+ah/x)^2)
The minimum of that function is not changed if we leave out the sqrt and the derivation of (x+a)^2+(h+ah/x)^2 is (2 (a + x) (-a h^2 + x^3))/x^3
So the minimum x is where this function equals zero, which is if x³ = ah²,
and the length then is L = (a^(2/3) + h^(2/3))^3
Now the thing that I find strange. Please look at this drawing (which is not really correct because the two "y" do not have the same length).
If the angle ACD is 90° then the ladder has minimal length!
We know that ah=xy, so let's square that: a²h²=x²y² and because ACD is 90° xa=y² which yields
a²h²=x²xa and that gives x³=ah² which is exactly what we got by using the calculus.
Do you have a geometric explanation why L is minimal if ACD is 90°?




